Tracing Attention Computation Through Feature Interactions

Transformer-based language models involve two main kinds of computations: multi-layer perceptron (MLP) layers that process information within a context position, and attention layers that conditionally move and process information between context positions. In our recent papers we made significant progress in breaking down MLP computation into interpretable steps. In this update, we fill in a major missing piece in our methodology, by introducing a way to decompose attentional computations as well.

Our prior work introduced attribution graphs as a way of representing the forward pass of a transformer as an interpretable causal graph. These graphs were built on top of (cross-layer) transcoders, a replacement for the original model’s MLP layers that use sparsely active “features” in place of the original MLP neurons. The features comprise the nodes of the attribution graphs, and edges in the graphs represent attributions – the influence of a source feature on a target feature in a later layer.

The attribution graphs in our initial work were incomplete, in that they omitted key information about attentional computations. The feature-feature interactions we studied – the edges in the graph – are mediated by attention heads that carry information between context positions. However, we did not attempt to explain why the attention heads attended to a particular context position. In many cases, this has prevented us from understanding the crux of how models perform a given task.

In this update, we describe a method to address this issue by extending attribution graphs so they can explain attention patterns. Our method is centered on “QK attributions,” which describe attention head scores as a bilinear function of feature activations on the respective query and key positions. We also describe a way to integrate this information into attribution graphs, by computing the contribution of different attention heads to graph edges.

We provide several case studies of this method in action. Some of these examples confirmed existing hypotheses we described in Biology, which we could not validate at the time:

• In an induction prompt, the query-side “X” features interact with key-side “preceded by X” features to cause induction heads to attend to the appropriate token.
• In a prompt where the model is asked for the opposite of a word, key-side features “tag” the relevant word so that query-side “opposite” features can find it at the appropriate time.
• In a multiple choice question, we confirm that interactions between “answer a multiple choice question” features and “correct answer” features cause “correct answer” attention heads to attend to the appropriate option.

We also surfaced new, unexpected mechanisms:

• How “concordance/discordance heads” are used to sanity-check statements.
• How attentional circuits employ many computations and heuristics operating in parallel, even in simple contexts. Some examples:

• In our induction prompt, the core induction mechanism coexists with a general “attend to names” mechanism.
• In the multiple choice prompt, the core “find the correct answer” mechanism is complemented by an “attend to any answer at all” mechanism.

The case studies here are our first attempts at applying the method, and we expect more discoveries to result in future work.

We believe the addition of QK attributions is a significant qualitative improvement on our original attribution graphs, unlocking analyses that were previously impossible. However, there remain many open research questions regarding attentional circuits, which we describe at the end of the post.

The problem: transcoder-based attribution graphs omit attentional computations

Transcoders only ever read and write information within the same context position – however, transformer models also contain attention layers, which carry information across context positions. Thus, the influence between any two transcoder features is mediated by attention layers For features in different context positions, all of the interaction is attention-mediated. For features in the same context position, some of the interaction is direct, and some is mediated by attention to the same position.

To make attribution a clearly defined operation, we designed our attribution graphs so that interactions between features are linear. One of the key tricks in doing this is to freeze the attention patterns, treating them as a constant linear operation (and ignoring why they have those attention patterns). This allows us to trace the effect of one feature on another through attention heads. This could potentially involve multiple attention heads operating in parallel, and also compositions of attention heads. The resulting attribution is a sum of attributions corresponding to the features being mediated by different sequences of attention heads.

But freezing attention patterns and summing over heads like this means our attribution graphs are “missing” key information about attentional computation, in two respects:

• The graphs left it ambiguous which (sequences of) heads were strongly involved in mediating a given edge.
• Even if we did identify the important heads, we failed to explain the mechanistic source of each head’s attention pattern – how the QK circuit of each head gave rise to its pattern. Indeed, by conditioning on attention patterns when computing gradients, our graphs ignored QK circuits entirely.

In our original paper, we pointed out that for many prompts, this missing QK information renders attribution graphs useless. In particular, for many prompts, the question of which head(s) mediated an edge, and why those heads attended where they did, is the crux of the computation. We provide several examples of this failure mode later in the paper and demonstrate how our method fills in the missing information.

High-level strategy

Explaining the source of an attention head’s attention pattern. The core insight underlying our method is the fact that attention scores (prior to softmax) are a bilinear function of the residual stream at the query and key positions. Thus, if we have a decomposition of the residual stream as a sum of feature components, we can rewrite the attention scores as a sum of dot products between feature-feature pairs (one on the query position, one on the key position). We call this decomposition “QK attribution” and describe in more detail how we compute it below. Note that the same strategy was used by and to analyze QK circuits, but explored in less depth.

Explaining how attention heads participate in attribution graphs. Explaining the source of each head’s attention scores is insufficient on its own; we also must understand how the heads participate in our attribution graphs. To do so, for each edge in an attribution graph, we keep track of the extent to which that edge was mediated by different attention heads. To achieve this, (cross-layer) transcoders on their own are not adequate; we explain this issue and how to resolve it below.

QK attributions

QK attributions are intended to explain why each head attended where it did. In this section, we assume that we have trained sparse autoencoders (SAEs) on the residual stream of each layer of the model (though there are alternative strategies we could use; see below).

In a standard attention layer, a head’s attention score at positions (p_k, p_q) is produced by taking the dot product of linear transformations of the residual stream at these positionsIn this update we focus on describing the QK attributions logic for vanilla attention layers. In some attention variants, this assumption does not quite hold – for instance, the commonly used rotary positional embeddings involve modifying the linear transformation depending on the context position, and thus attention scores will be influenced by positional information not present in the residual stream. In general, however, the basic premise of QK attributions can be extended to all common attention architectures we are aware of. To simplify things, we introduce a matrix W_{QK} = W_Q^T W_K (see discussion in the Framework paper). We simply expand the key and query activations to describe them in terms of feature activations (along with a bias and residual error), and then multiply out the bilinear interaction:

The sum of these terms adds up to the attention score.

Note that in some architectures, there may exist a normalization step between the residual stream and the linear transformations W_Q and W_K. In this case, the feature vectors should first be transformed by linearization of the normalization layer before being used in the above formulae. If the normalization layer involves a bias term, it can be folded into the bias term above.

Once we have computed these terms, we can simply list them ordered by magnitude. Each term is an interaction between a query-side and key-side component, which can be listed side-by-side. For feature components, we label them with their feature description and make them hoverable in our interactive UI so that their “feature visualization” can be easily viewed.

One limitation of this approach is that it does not directly explain the attention pattern itself, which involves competition between the attention scores at multiple context positions – to explain why an attention head attended to a particular position, it may be important to understand why it didn’t attend to other positions. Our method gives us information about QK attributions at all context positions, including negative attributions, so we do have access to this information (and we highlight some interesting inhibitory effects in some of our later examples). However, we do not yet have a way of automatically surfacing the important inhibitory effects without manual inspection. While addressing this limitation is an important direction for future work, we nevertheless find that our attention score decompositions can be interpretable and useful.

Computing attention head contributions to an attribution graph

QK attributions help us understand the source of each head’s attention pattern. For this understanding to be useful to us, we need to understand what these attention patterns were used for. Our strategy is to enrich our attribution graphs with “head loadings” for each edge, which tell us the contributions that each attention head made to that edge.

“Checkpointing” attention paths with features

It turns out that computing the contributions of attention heads to graph edges is difficult to achieve with transcoder-based attribution graphs. This is because when transcoder features are separated by L layers, the number of possible attention head paths between them grows exponentially with LNote that this issue is not resolved by using cross-layer transcoders. Thus, it is computationally difficult Though potentially an interesting problem for future work – plausibly a search algorithm could be used to identify important paths. to decompose edges in transcoder-based attribution graphs into their contributions from each path.

We can sidestep this issue by using a method that forces each edge in a graph to be mediated only by attention head paths of length 1. This can be achieved using several different strategies, which we have experimented with:

1. By using Multi-Token Transcoders (MTCs), a transcoder-like replacement for attention layers. MTC features are “carried” by (linear combinations of) attention heads, rather than paths through multiple attention heads, and thus do not suffer the exponential-number-of-paths issue.
2. By training SAEs on the output of each attention layer, and including these features as nodes in attribution graphs alongside (cross-layer) transcoder features. This “checkpoints” attributions through each attention layer, eliminating all attention head paths of length greater than 1.
3. By training SAEs on the residual stream at each layer of the model, and computing gradient attributions between features at adjacent layers. This also “checkpoints” attributions at each layer in the same way as the previous options.

• In practice, instead of SAEs at each residual stream layer, we compute these graphs using weakly causal crosscoders (WCCs), whose features read from the residual stream at a residual stream layer L, and reconstruct the residual stream at layers L, L+1, …, num_layers Note that WCCs are not intended to replace nonlinear model computation, but rather to decompose representations (like SAEs) while also capturing information that is linearly propagated across layers.. Given a target feature in a layer K, we compute gradients from its layer-K decoder vector to the layer K−1 residual stream, and compute the dot product of this gradient with source feature projections (activation times decoder vector) in layers K−1. However, those decoders may belong to features that originated at earlier layers, allowing us to “hop back” across layers and avoid long chains of redundant features (similar to the motivation for cross-layer transcoders).

For now, we have adopted the third strategy. The other two methods accumulate error in the residual stream across layers, which we have found leads to greater overall reconstruction errors, resulting in attributions that are dominated by error nodes. Note, however, that this choice has a tradeoff, which is that our attributions through MLP layers are no longer linear as they are in transcoder-based attribution graphs. As a result, we run the risk of attributions being uninterpretable, or highly “local” to the specific input prompt. In subsequent exposition, we will describe our algorithm as applied to residual stream SAE-based graphs (the extension to WCCs is straightforward).

It’s important to note that an edge may still be mediated by multiple heads at a given layer! However, it can no longer be mediated by chains of heads across multiple layers.

Head loadings

Once we have trained SAEs (or a suitable alternative) as described above, we can compute attention head loadings for graph edges – the amount that each head is responsible for mediating that edge. Any edge between two SAE features in adjacent layers is a sum of three terms: an attention-mediated component, an MLP-mediated component, and a residual connection-mediated component.

Let source and target feature at positions p_s and p_t, with activations a_s and a_t, and feature vectors \mathbf{v_s} and \mathbf{v_t}The feature vectors correspond to the decoder weights of the SAE. When making attribution graphs with SAEs, unlike transcoders, we ignore the SAE encoders. The encoders in transcoder-based graphs correspond to weights of a “replacement model,” but in SAE-based graphs they have no such interpretation, and we think of them as just a tool to infer feature activations.. The attention-mediated component can be written as follows.

\sum_{h \in \text{heads}} a_s a_t \left(\mathbf{v_t}^\top O_h V_h \mathbf{v_s}\right) \cdot \text{attention}_h(p_s, p_t)

The sum over heads runs over all the heads in the source feature’s layer (which is one layer prior to the target feature’s). Each term in this sum represents the contribution (head loading) of a specific attention head to this edge. We compute and store these terms separately and surface them in our UI .

Examples

In this section, we will show how head loadings and QK attributions can be used to understand attentional computations that were missing in our previous work.

Induction

Claude 3.5 Haiku completes the prompt:

with “Sally”. In our original paper, the attribution graph for this prompt shows a strong direct edge from “Sally” features (on the “Sally” token) to the “Sally” logit on the final token. In other words, the model said “Sally” because it attended to the “Sally” token. This is not a useful explanation of the model’s computation! In particular, we’d like to know why the model attended to the Sally token and not some other token.

Prior work has suggested that language models learn specific attention heads for induction, but it’s unclear how these heads perform the induction mechanism. In this example:

1. How does the model decide to carry “Sally” over to the second “Aunt” token? When we looked at this prompt’s attribution graph before, we saw that the behavior described here definitely happened in the OV circuit – i.e. a “Sally” feature is used at the target context position, and is attributed to the previous “Sally” token.
2. How does “Aunt” information get moved to the first “Sally” token?

We used QK attributions to investigate both questions.

Transforming “Sally” to “say Sally” on the second “Aunt” token

To answer the first question, we traced the input edges of the “Sally” logit node and “say Sally” features on the second “Aunt token.”  We find that these nodes receive inputs from “Sally” features on the “Sally” token, and that these edges are mediated by a small set of attention heads. When we inspect the QK attributions for these heads, we find interactions between:

• Features representing “Aunt” or “Aunt / Uncle / other family signifiers” on the query side
• Two categories of features on the key side:

• Features representing names (either names in general or “Sally” specifically)
• Features representing “this is the name of an Aunt / Uncle” that activate on name tokens following “Aunt” or “Uncle”

Thus, the QK circuit for these induction-relevant heads appears to combine two heuristics: (1) searching for any name token at all, (2) searching specifically for names of aunt/uncles.Note that we label heads in diagrams based on the role they play on the prompt we are studying. We generally do not expect heads to only be playing that role when studied over a broader distribution.

We performed interventions with this mechanism to test our hypothesis. We begin by choosing a set of heads with high head loadings (roughly 3-10% of headsWe hypothesize that the reason why we need to steer on many heads is because of the “hydra head” effect - if one head stops attending, another head in a downstream layer compensates by attending when it didn’t originally . Indeed, if we freeze the attention pattern for heads that we are not steering, we need fewer than half of the number of heads to produce the same effect. We leave a more detailed exploration of this effect for future work.) between the two tokens. On these heads, we scale the “Name of Aunt/Uncle” features from the “Sally” token only within the QK circuit for those heads, and measure how the model changes its prediction as well as how the attention pattern of the important heads change. We see that removing this feature from the key side completely removes the model’s induction capability, and the model predicts generic Aunt names instead.

Copying “Aunt” to “this is the name of an Aunt” on the “Sally” token

To answer the second question, we looked at all edges in the pruned graph between the first “Aunt” token and the first “Sally” token. There are many edges which connect features between these two tokens, but most of them appear to be doing the same thing: connecting an “Aunt” feature to a “last token was Aunt” feature. If we look at the head loadings for these edges, nearly all high-weight edges are mediated by the same subset of heads.

Next, we looked at the QK attributions for these heads. All the relevant heads’ attention scores seem to be predominantly explained by the same query-key interactions – query-side “first name” features interacting with key-side “title preceding name” features (activating on words like “Aunt”, “Mr.”, etc.).

Note that so far, we’ve ignored the effect of positional information on attention pattern formation, but we might expect it to be important in the case of induction – for instance, if there are multiple names with titles mentioned in the context, the “Sally” token should attend to the most recent one. We leave this question for future work.

Multiple parallel QK interactions

In the examples above, we depict attention scores as being driven by an interaction between a single type of query-side and key-side feature. In reality, there are many independent query feature / key feature interactions that contribute. Below we show an example where some of the multiple independent interactions are particularly interesting and interpretable.

In the prompt

which Haiku completes with “Sue”, we see that query-side “Mary” features interact with key-side “token after ‘Mary’” features, and, independently, we see that query and key-side “Name of Aunt/Uncle” features interact with one another. Notably, we do not see strong contributions from the cross terms (e.g. “Mary” interacting with “Name of Aunt/Uncle”) – that is, the rank of this QK attributions matrix is at least 2. In reality, even this picture is a dramatic oversimplification, and we see several other kinds of independently contributing QK interactions (for instance, the bias term on the query side interacting with generic name-related features on the key side, suggesting that these heads have a general bias to attend to name tokens).

Antonyms

Haiku completes the prompt Le contraire de "petit" est " with “grand” (“The opposite of ‘small’ is ‘big’”, in French).

In our original paper, the attribution graph for this prompt showed edges from features representing the concept of “small” onto features representing the concept of “large.” Why does this small-to-large transformation occur? We hypothesized that this may be mediated by “opposite heads,” attention heads that invert the semantic meaning of features. However, we were not able to confirm this hypothesis, or explain how such heads know to be active in this prompt.

After computing head loadings and QK attributions, we see that the small-to-large edges are mediated by a limited collection of attention heads. When we inspect the QK attributions for these heads, we find two interesting interactions between the following kinds of features:

• On the key-side

• Features active on tokens for which an opposite or alternative being requested (often active on “X” in the phrase “opposite of X” or “alternatives to X”)
• Features active generically on adjectives / modifiers

• On the query-side:

• Features active in contexts that discuss opposites / antonyms

This suggests that the model mixes at least two mechanisms:

• One which explicitly tags the word “petit” as the word whose opposite is being asked for
• One which simply searches for any plausible adjective whose opposite could be computed

We find that inhibiting the query-side “opposite” features significantly reduces the model’s prediction of “large” in French, and causes the model to begin predicting synonyms of “small” such as “peu” and “faible”. A similar (but lesser) effect occurs when we inhibit “adjective” features on the key side.

Multiple Choice

Haiku completes the prompt

with “B”.

In our original paper, the attribution graph showed a direct edge from “B” features on the “B” token to the “B” logit on the final token (or to “say B” features in the final context positions, which themselves upweight the “B” logit). Again, this is not a helpful explanation of the model’s computation!  We want to know how the model knew to attend to the “B” option and not one of the other options. We hypothesized (inspired by ) a mechanism in which (1) “B” information was copied over to the “1945” token, (2) a “correct answer” feature is active on the 1945 token, (3) a query feature on the final context position interacts with the “correct answer” feature to attend to the 1945 token, and copies the “B” information via the OV circuit. (4) the “B” information then leads downstream attention heads to attend to the “B” token. However, our attribution graphs could not be used to test this hypothesis.

How does the model know to attend to the tokens associated with option B? To answer this question, we inspected the head loadings for these edges and found a fairly small collection of heads that mediate them. Inspecting the QK attributions for these heads, we found interaction between:

• On the query side:

• Features that activate when the model needs to say an answer or a specific piece of information (e.g. the “is” in “The correct answer is”, “” as a tag introducing a multiple choice answer, open-parentheses tokens introducing parentheticals that specify quantitative figures)
• The bias term

• On the key side:

• “Correct-answer” features that activate on the tokens associated with the correct answer to multiple choice questions
• “False statement” features that activate on the tokens for incorrect answers, which interact negatively with the “say a multiple choice” features described above to inhibit the attention score
• Features that generically activate on tokens of multiple choice response options

These interactions suggest that these heads have an overall inclination (due to the query-side bias contribution) to attend to correct answers at all times, and an even stronger inclination to do so when the context suggests that the model needs to provide a multiple choice answer.

We validated this mechanism with the following perturbation experiments:

• Inhibiting the “correct answer” features on the key-side tokens inhibit the model’s “B” response
• Activating the “correct answer” features on tokens corresponding to a different option causes the model to flip its output to the corresponding letter

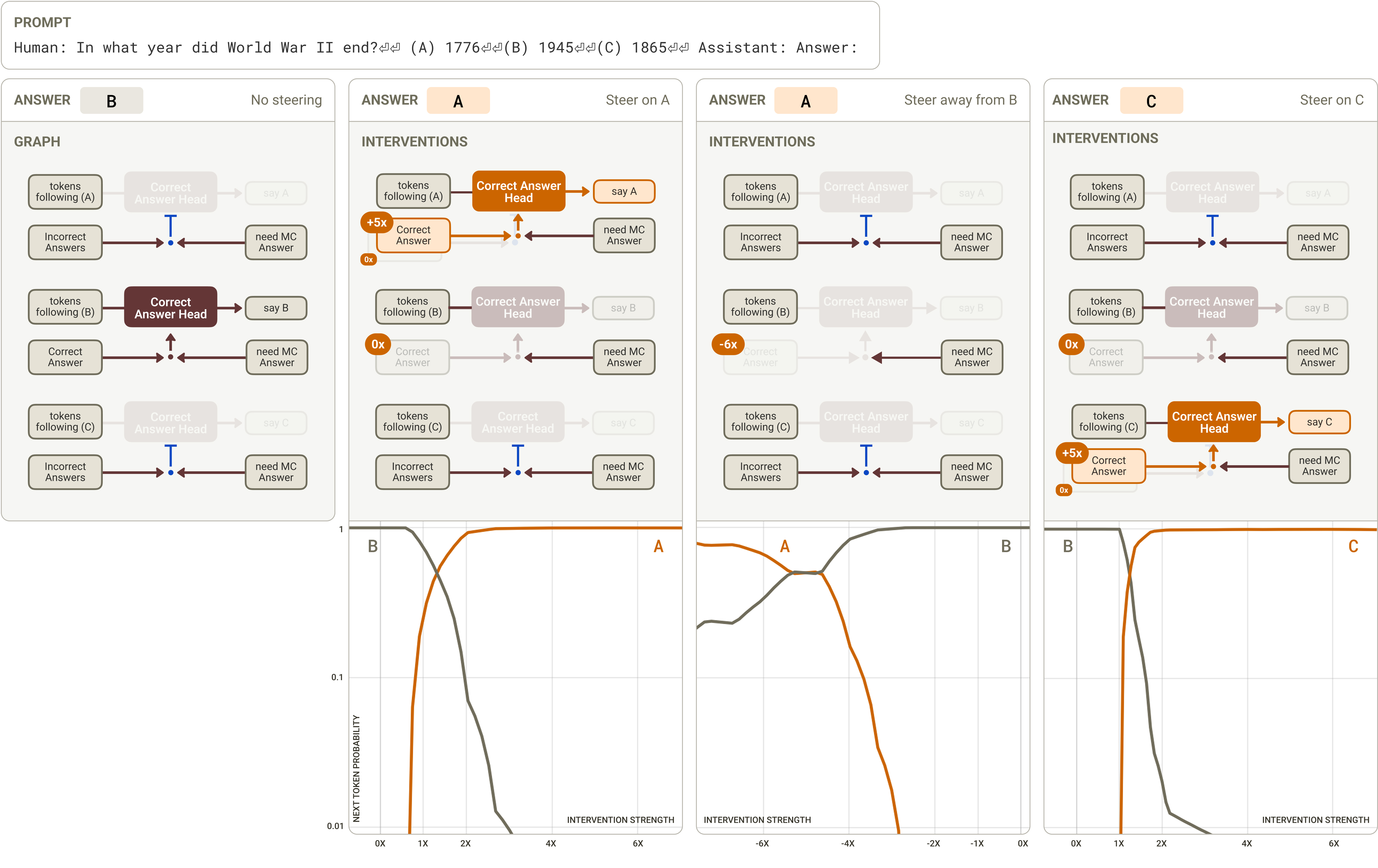
To complete our understanding of the model’s computation on this prompt, we would like to understand how the “correct answer” features are computed in the first place. The graph suggests that these features emerge from a combination of two sets of features: “1945 (in the context of ‘the end of World War 2’)” features over the same token, and “end of World War 2” features over the relevant tokens in the question. Unfortunately, we are not able to understand the mechanism in more depth as the cross-token inputs are obscured by error nodes.

Correctness circuits

Haiku completes the prompt

with “Yes”. If yellow is replaced with red, it answers “No”.

How does the model distinguish between the correct and incorrect statements? Surprisingly, we did not find clear evidence of our initial hypothesis: that the model first explicitly computes color + banana = yellow and then matches the stated answer, yellow or red, with the computed answer. Instead, we found distinct attention heads which directly determine the concordance or discordance of the stated answer with respect to the posed computation.

Tracing back from the “Yes” and “No” responses in the respective attribution graphs, we observed “correct answer” features (in the yellow case), and “false statements about equalities” (in the red case). These in turn received inputs from a “plausible properties of things” feature (in the yellow case) and a “discordant statements” feature (in the red case). These features are only active in their respective prompts, and not the other.

Interestingly, when we trace back from the “plausible properties” and “discordant statements” features, we observe that they receive strong inputs from features on the “banana” token. These features include a variety of fairly generic noun-related features (such as “nouns after descriptors”) in addition to some of the “banana” features. The specific input features vary somewhat between the two prompts, but not in a way that makes it clear why they would be triggering “plausible properties” in one case and “discordant statements” in another.

However, we noticed that the attention heads carrying these edges were different in the two cases. One set of heads (“concordance heads”) carried the edge in the yellow case, while another set of heads (“discordance heads”) carried the edge in the red case.

When we inspected the QK attributions for these heads, we saw that these heads were driven by interactions between the relevant color features (yellow or red) on the query side, and banana features on the key side. Banana-yellow interactions contributed positively to the concordance heads’ attention score and negatively to the discordance heads’ attention score; banana-red interactions did the reverse.

Thus, we arrived at the following understanding of the circuit.

To test the mechanistic faithfulness of this circuit, we performed causal interventions on the concordance and discordance heads. We tested whether steering on the QK-attributed features could shift the attention patterns of the heads and the resulting response of the model. Using the ‘banana is yellow’ prompt, we steered the query-side input to the concordance and discordance heads, positively steering on one ‘red’ feature with concurrent negative steering on one ‘yellow’ feature. This was sufficient to reduce attention of the concordance heads from the yellow context position to the banana context position, while increasing attention of the discordance heads between the same positions. In turn, this targeted intervention was sufficient to flip the model’s response from Yes to No, even at moderate steering values. Additional interventions showed that the scaled output of even a single concordance or discordance head is sufficient to flip the response, and that this effect is strengthened through the combination of multiple such heads. Notably, larger steering magnitudes were required on concordance heads to flip the answer from “No” to “Yes” than on discordance heads to flip the answer from “Yes” to “No”. One possible picture that emerges from these experiments is that “more things have to go right” for a stated answer to be deemed correct. Multiple concordance heads may work together to check the validity of different facets of a stated comparison, and only if all these boxes are checked is the answer deemed correct. This process is reminiscent of how people can use heuristics to determine whether a stated answer is correct. For instance, a person can quickly determine that 24*4 = 1023331 is false, without actually actually computing 24*4, simply by estimating the order of magnitude of the answer or determining that the answer must be even. These facets might represent the types of assessments performed by different concordance heads. In contrast, when a discordance head is activated it may represent a strong signal that the answer could not possibly be correct.

We have also observed that the same heads play similar roles in checking other kinds of correctness. For instance, consider the prompt

Which the model completes with “Yes”. If 5 is replaced with 6, it answers “No”.

When we inspected the attention patterns from the “23” token to the second operand token (“5” or “6”), we observed that the same “concordance heads” and “discordance heads” appear to discriminate between correct and incorrect cases in the expected way (higher attention pattern for the concordance head in the correct case, and vice versa for the discordance head).

When we inspect the QK attributions for these heads, we observed “numbers separated by an interval of 5” features on the query side interacting with “5” and “6” features on their respective prompts. In the “5” case, the contributions of these interactions to the attention score were positive for the concordance heads and negative for the discordance heads. In the “6” case, the signs were reversed.

Notably, in this case we also did not see clear evidence of the model first explicitly computing the answer (23 or 24, respectively), and then matching it with the stated answer, 23. The model instead identifies a “property” of the sum x+y, by using its ability to recognize sequences incrementing by 5 to determine that the second term should be 5, and uses the concordance and discordance heads to detect that property.

Thus, our preliminary conclusion is that these heads use their QK circuits to check for concordant properties between features on the query and key tokens. For the concordance head, if there is a QK match, it attends to the relevant key token.Corroborating this picture, we found that feature-feature interactions through the W_{QK} matrix skew positive for the concordance heads and negative for discordance heads. We also note that this property can be checked without reference to the feature basis–we noticed that the eigenvalues of the W_{QK} matrix skew positive for the concordance heads and negative for the discordance heads. Its OV circuit transforms attribute-related key-side features into “plausible property” query side features. For the inconsistency head, if there is a QK mismatch, it attends to the relevant key token, and its OV circuit transforms attribute-related key-side features into “discordant statement” query side features. These features are then transformed into the correct/incorrect features we originally traced from.

More work is needed to understand the scope and generality of which kinds of properties these heads can check for, and what exactly the OV circuit is using as input substrate to transform into (in)correctness-related outputs.

Related work

The work most closely related to ours is , which computed QK attributions for some important heads in the indirect object identification (IOI) task , and analyzed them in the context of transcoder-based attribution graphs. In this work, the important heads were identified based on the manual analysis conducted by rather than using a systematic head loadings computation (and thus they did not run into the “checkpointing” problem that we address in this work). also computed QK attributions, and in fact trained SAEs incentivized to make the QK attributions sparse, using a sparsity-penalized learnable mask on the feature-feature interactions. studied the use of attention out SAEs for attention circuit analysis; as part of this work, they conducted an analysis of QK attributions (of features propagated by OV circuits that go onto interact with key-side features via QK circuits).

Other papers have studied QK circuit mechanisms using carefully designed patching experiments. For instance, studied QK circuits underlying entity binding, investigated QK circuits in multiple choice question answering, and identified QK circuits involved in IOI.

Future work

Head loadings and QK attributions provide a simple, albeit somewhat brute force, way of explaining where the attention patterns came from that facilitated edges in an attribution graph. This ability has proved useful in understanding behavior that was previously left unexplained, and we plan on investing in it further. We’re interested in simply applying this method to a broader range of examples to better understand attention “biology” – some applications of particular interest include understanding entity binding, state tracking, and in-context learning.

We’re also interested in improving the methodology. Some questions of interest include:

• Can QK attribution information be distilled or simplified? Preliminary analyses suggest that the QK attributions matrix for a given head at a given query-key position pair is typically approximately low-rank. This could allow us to replace a lengthy list of feature-feature interactions with a shorter list of interactions between “feature components” (linear combinations of related features).

• Our QK attributions explain attention scores, but attention patterns involve an extra softmax step which introduces competition between context positions. Thus, to explain why an attention head attended to a particular position, it can be important to understand why it didn’t attend to other positions. In principle, QK attributions can give us this information – we can look at feature-feature terms that make negative contributions to the attention scores at other key positions for the same query position. However, it is unclear how to identify the most important negative contributions in an automated fashion–in some ways, this reduces to the problem of identifying the “relevant counterfactuals” on a given prompt.

• How can we scale head loadings and QK attributions to long contexts? Naively, the computation scales quadratically with context length. To circumvent this, we likely need some kind of dynamic pruning algorithm that only computes this information for important edges / heads.

• If we look at a given head’s QK attributions, and the edges mediated by its OV circuit, across prompts, will we find it performing “the same algorithm?”  Or are individual heads “polysemantic,” performing qualitatively different kinds of computations in different circumstances? If so, how can we break them up into their distinct subcomponents?

• When an edge is mediated by multiple heads at a time, are those heads typically attending “for the same reason” (i.e. are their QK attributions similar), suggesting attention head superposition? How do we best identify functional attention units that may be distributed across heads? Some transcoder-like approach to replacing attention layers may be useful here, but finding the right decomposition strategy has proven challenging.

We’d be excited to see the community explore these and related questions, and to extend the open-source attribution graph repo and interface to include attentional attributions.